
Conţinut
- Legea lui Zipf a explicat
- Experimentul de bază
- Legea Zipf în piețele de aburi
- Ce putem afla despre Steam?
- concluzii
Cu puțin timp în urmă, un prieten de-al meu mi-a sugerat să urmăresc videoclipul lui Vsauces despre legea lui Zipf, principiul lui Pareto și aparențele misterioase din jurul lui. Iată un mic teaser pentru a vă atrage atenția - 80% din toți oamenii trăiesc în 20% din cele mai populare orașe; 80% din toate terenurile aparțin 20% dintre cei mai bogați proprietari; 80% din toate coșurile de gunoi se află pe primele 20% dintre străzile cele mai trasnite - așa cum prevede legea lui Zipf și principiul Paretos.
Insuficient? Ei bine, după cum am descoperit ieri, gaura de iepure nu se oprește acolo ... Splendid de scepticism, am decis să văd cât timp oamenii petrec jocurile Steam ... Ei bine. 80% din timpul oamenilor este petrecut jucând 20% dintre cele mai populare jocuri ... Interesant? Ei bine, citiți mai departe, există mai multe despre această poveste.
Cu începere de peste 20 de minute, efortul lui Vsauces este minunat și explică o mulțime de chestii despre Zipf, cu toate acestea el este foarte timid să ne arate mecanismul de bază despre care se crede că se comportă de ce Zipf funcționează cum o face. Așadar, înainte de a continua, aș dori să explic pe scurt acest lucru.
Legea lui Zipf a explicat
Există mai multe moduri conceptuale de a explica intuiția din spatele principiului 20/80. Cel mai bun exemplu, în opinia mea, este cel al craterelor Lunii.
Experimentul de bază
Deci, imaginați-vă dacă vreți, că există o Lună neatinsă - o suprafață perfect netedă. Acum, spuneți că există niște asteroizi de dimensiuni aleatorii care l-au lovit pe Lună. Când primul asteroid se așează, acesta lasă un crater. Acum încă o lovit, lăsând un crater în altă parte. Fiecare crater este o parte a suprafeței totale, prin urmare, există șansa ca următorul asteroid aleator să lovească aproape un crater existent și să se alăture cu acesta, formând un grup. Șansa unui nou asteroid care lovește un crater dat este proporțională cu dimensiunile existente ale craterelor și asteroizilor. Acest lucru înseamnă că următorul asteroid aleator este mai probabil să se alăture celui mai mare grup existent, făcându-l chiar mai mare. Un fel de proces cumulat, care creează apoi un mecanism rich-get-richer sărac-primi-lonelier.
Țineți minte acest lucru, deoarece se crede că aceasta este explicația generală pentru "de ce" legea Zipfs funcționează cu o asemenea universalitate misterioasă. Exemplul asteroidului este destul de simplu, însă întrebarea este ce se va întâmpla în timpul mai multor repetări
Un pic uluitor?
Ei bine, am făcut un gif pentru a conduce acest punct inițial acasă. NB! graficul va fi discutat mai târziu, încercați doar să fotografiați experimentul.

Dacă observăm Luna actuală, se constată că, deoarece cantitatea de asteroizi crește la cantități mari, diametrele craterului observate cresc astfel încât primele 20% din cele mai mari cratere se apropie de 80% din suprafața totală.
Deci, pe măsură ce mergem la mai mulți asteroizi, distribuția celor mai populare și mai puțin populare grupuri se apropie de un fel de "distribuție ideală" cu această proprietate 20/80 - o distribuție Pareto. Dacă faceți matematica, se pare că (în general), dacă cel mai mare grup are dimensiunea N, al doilea cel mai mare grup este în jurul dimensiunii N / 2, al treilea N / 3 și așa mai departe și așa mai departe. Aceasta se numește Legea lui Zipf. Lucrul ciudat este distribuția legii și distribuției Pareto a Zipf pentru o sumă uluitoare de elemente (asteroizi) și grupuri (grupuri de crater). Desigur, există încurcări și tulburări aleatorii, însă tendința generală este incontestabilă.
Sper că puteți vedea cum este mai probabil ca asteroizii să lovească craterele mari de pe Lună, făcând legătura cu orașele să fie mai atractive, dacă există deja mai mulți oameni care trăiesc în ele. Cu toate acestea, trebuie să realizăm că orașele sunt departe de singurele "grupuri" care se comportă în conformitate cu Zipf.
Iată câteva exemple din cercetarea lui Mark Newmans despre distribuțiile Pareto. NB! Graficele sunt în scară log-log care elimină forma hiperbolică a curbelor, prezentând o relație aproape liniară.
Inițial y = aX ^ (- b)
Jurnalele ambelor părți => log y = log a - b log X
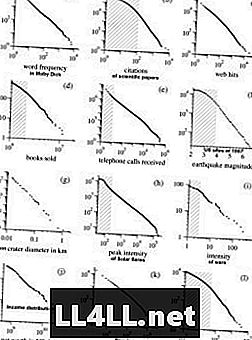
În mod interesant, aceeași tendință este afișată și de cultele religioase ... Proprietatea comună a majorității acestor fenomene este pur și simplu această tendință "de grupuri mari". Deci, legea lui Zipf este persistentă în mecanisme, în care preferințele elementelor sunt legate în mod pozitiv de mărimea grupurilor (adică, cu cât grupul este mai mare, cu atât mai probabil va crește). De aceea îmi place să mă gândesc la grupuri ca grupuri și elemente ca grupări.
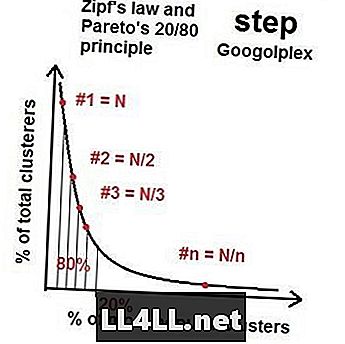
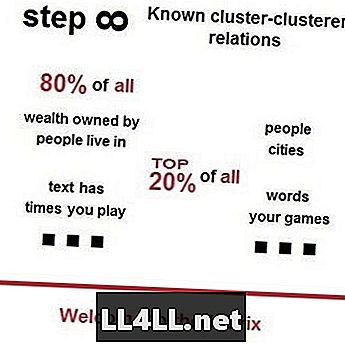
Legea Zipf în piețele de aburi
Suspecte de ultima? Iată cantitatea de timp petrecută de oameni pentru cele mai populare jocuri de pe Steam .. Datele de la SteamSpy.
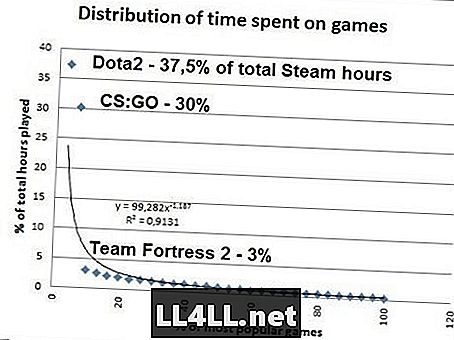
Dacă faci matematica, se pare că 20% dintre cele mai populare jocuri Steam reprezintă 80% din suma totală de joc, astfel încât misterul Pareto 20/80 funcționează ca un farmec aici ... Trebuie observat totuși că pentru Zipf este adevărat, CS: GO trebuie să reprezinte 37,5% / 2 = 18,8% din timpul total, în loc de 30%. Dar în afară de acest outlier (STOP JLAYING CS: GO), distribuția asemănătoare Zipf este clar acolo.
Iată cantitatea de copii vândute pentru cele mai populare jocuri.
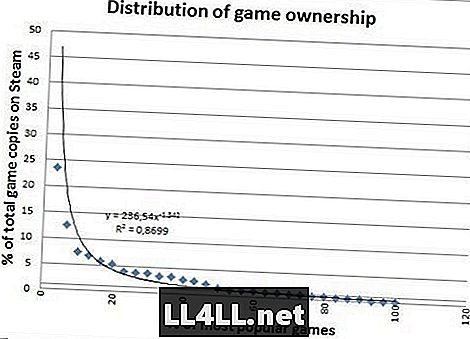
Se pare mult mai frumos eh? Copiile vândute nu au margini mari, așa că se potrivesc foarte bine, ceea ce este o diferență notabilă. Totuși, este ceva mai interesant de dedus din diferențele dintre ultimele două grafice.
Observi cum arată "coada" spre dreapta un fel de grăsime în al doilea grafic? Ei bine, în termeni simpli, acest lucru ne spune că jocurile "relativ nepopulare" sunt de fapt mult mai populare decât în complotul anterior.
De fapt, se pare că 20% dintre cele mai populare jocuri reprezintă doar 60% din vânzări, față de 80% din joc. Interesant? Pariezi că fundul tău este.
Ce putem afla despre Steam?
Ei bine, faptul că popularitatea jocului urmează distribuției Pareto ne spune că, într-adevăr, există un fel de efect pozitiv al rețelei, ceea ce face jucătorii să aleagă jocuri care sunt deja jucate de mai mulți oameni. Ceea ce diferența în ceea ce privește grăsimea cozilor ne spune că utilizatorii Steam sunt mult mai "orbiți în grup", atunci când cumpără jocuri decât atunci când le joacă.
Gândiți-vă - cu cât mai mulți oameni cumpără jocuri, indiferent de "opinia populară actuală", cu atât mai mult devine distribuția distribuției Pareto, deoarece este mai puțin probabil ca jocurile mari să crească în continuare. Dacă nimeni nu a dat un șobolan în jurul valorii de cât de mulți oameni joacă deja un joc și disponibilitatea tuturor jocurilor a fost aceeași, atunci ne-am aștepta ca 20% dintre cele mai populare jocuri să reprezinte aproximativ 50% din vânzări și timpul de joc (de exemplu, distribuite normal).
concluzii
Deci, există doi factori care contribuie la distribuția Pareto pe piețele Steam - cât de inovativi sunt dezvoltatorii (câte cratere de lună noi sunt formate) și cât de mult jucătorii (asteroizii) apreciază dimensiunea curentă a grupului atunci când aleg grupul care se va alătura . După cum se dovedește, jucătorii sunt foarte orbi de grup atunci când cumpără jocuri, ci doar opusul când le joacă. Tare nu?
Dacă doriți să aflați mai multe despre distribuțiile legii și puterii Zipf, aici este o prelegere frumoasă. În plus, asigurați-vă că aveți o privire la hârtia lui Newman!
Dacă vreți să citiți mai multe despre acest gen de lucruri, în curând voi încerca să vă alăturați acestei observații unui model care arată că jocurile multiplayer mai populare au prețuri mai mari (ceea ce leagă preferința gamerilor de a se alătura unor grupuri de dimensiuni mai mari). Vedeți articolul aici. Articolul Piece De Resistance va încerca să se alăture acestor teorii împreună explicând modul în care jocurile multiplayer, rețelele sociale și orașele sunt de fapt toate bunurile anti-rivale cu efecte de rețea (cu cât consumatorii consumă mai bine, cu atât mai mult beneficiază fiecare consumator individual) le-a înzestrat cu această mizerie zipfiană de mister ...
Până atunci - bucurați-vă!
P.S. Pop într-un comentariu cu o idee distractivă pentru o relație de 20/80 care credeți că ar putea fi adevărată.
Mina sunt:
80% din nostalgia popoarelor este cauzată de 20% din cele mai fericite amintiri (dovedite de fapt pentru rata de uitare a oamenilor)
80% din masă este concentrată în 20% din cele mai mari obiecte spațiale (dovedită efectiv pentru distribuția forței gravitaționale)
Și, desigur
80% din mizeria din toaletă provine de la 20% din ceea ce mănânci (nu se poate vorbi de cercetări academice)